Fractions to decimals
Fifths
Double the numerator and move the decimal to the left.
Example:
1/5 = .2
3/5 = .6
Sixths
Some of these fractions should already be familiar.
Example:
2/6=1/3=.333
3/6=1/2=.5
4/6=.6666
Sevenths
The sequence is the same for all decimals; only the order changes.
142857
Memorise the sequence and the initial digits for each fraction.
1/7 = .142857..
2/7 = .285714..
3/7 = .428571..
4/7 = .571428..
5/7 = .714285..
6/7 = .857142..
The tenths digit is equivalent to the numerator in the first two decimal conversions(1/7,2/7).
It is one greater in the next two, and two greater in the final two.
Eighths
Find half, or the closest quarter, and add or subtract 1/8 (.125).
2/8 = 1/4 = .25
3/8 = .25 +.125 = .375
4/8 = 1/2 = .5
5/8 = .5 + .125 = .625
6/8 = 3/4 = .75
7/8 = .75 + .125 = .875
Ninths
1/9 = .111...
2/9 = .222...
3/9 = .333...
:
8/9 = .888...
Tenths
1/10 = .1
2/10 = .2
3/10 = .3
:
9/10 = .909090
Elevenths
Assumes knowledge of multiples of nine.
1/11 = .090909...
2/11 = .181818...
3/11 = .272727...
4/11 = .363636...
:
9/10 = .909090...
Fractions to decimals division table
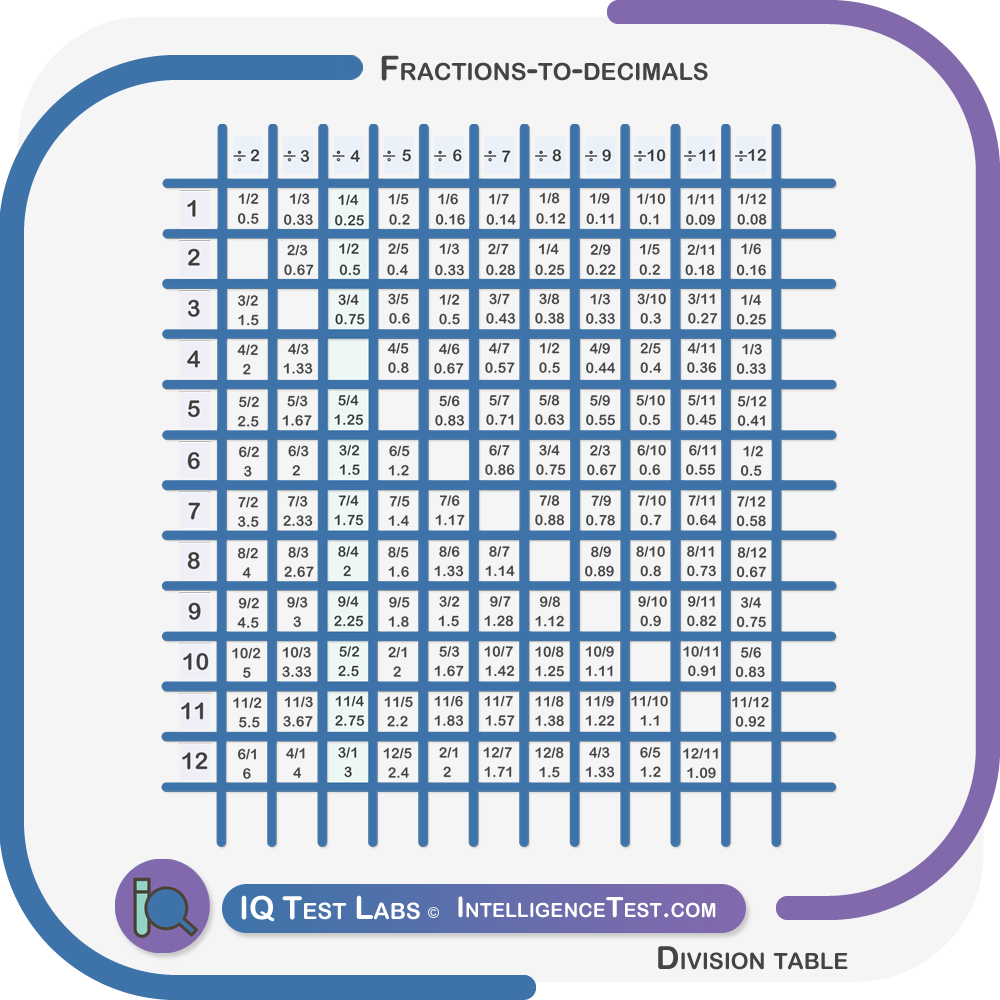
Refer to the ÷4 column of the division table. The difference between all numbers is 0.25.
In some columns there are occassional fluctuations in values due to rounding off. For example in the ÷9 column, the difference between most numbers is 0.11, and sometimes 0.12.
When converting to a decimal, refer to a known value in a column and then add or subtract the known difference.
Example: 11/4
The difference between numbers in the ÷4 column is 0.25.
Reference point: 12/4 or 3
3 − 0.25 = 2.75
Multiples
When a fraction is a multiple of a known decimal, new decimals can be calculated by multiplication or division.
Example 1: 7/16
If 7/8 is already known (.88), and 7/16 is half of 7/8.
then .88×1/2 = 0.44
Example 2: 1000/8
10/8 is already known (1.25)
For every multiple of ten, shift the decimal point to the right.
1000/8=125